TEOREMA DE PITÁGORAS

El teorema de Pitágoras da una relación entre la hipotenusa y los catetos de un triángulo rectángulo:

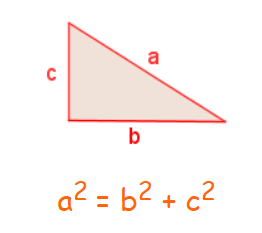
En todo triángulo rectángulo se verifica que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

TERNAS PITAGÓRICAS

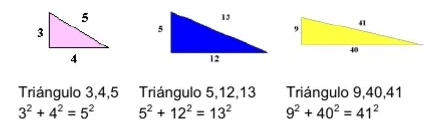
Las tres longitudes de un triángulo rectángulo cuando estas se corresponden a números naturales (números enteros, sin decimales) se llaman ternas pitagóricas.

Es decir una terna de números, (a, b, c), que cumplan el teorema de Pitágoras se dice que es una terna Pitagórica.

PRUEBA DE LOOMIS – AMPLIACIÓN DEL TEOREMA DE PITÁGORAS

En 1933, Loomis, matemático estadounidense, plantea una extensión del Teorema de Pitágoras en la que establece que:

La relación pitagórica se mantiene para cualquier polígono regular construido a partir de triángulos isósceles construidos sobre el triángulo inicial.

La propiedad pitagórica no es válida únicamente para los cuadrados de lados los catetos y la hipotenusa, sino para cualquier polígono construido sobre los lados del triángulo rectángulo, siempre que los tres polígonos, así construidos, sean semejantes entre sí.

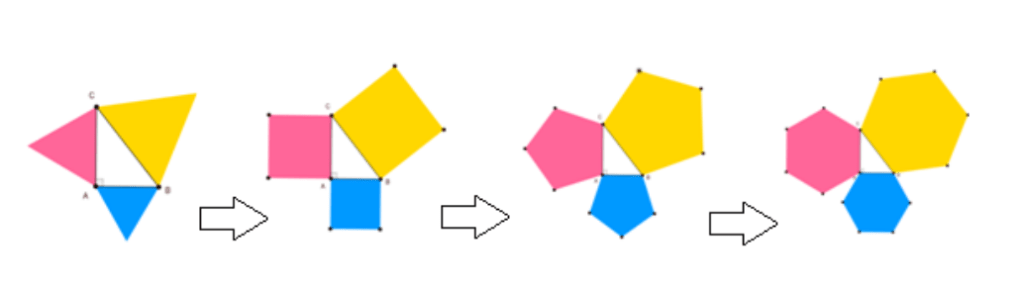
Se construye el triángulo rectángulo ABC (blanco)
Se construyen polígonos regulares sobre sus lados: triángulos, cuadrados, pentágonos, hexágonos, heptágonos, etc.
Se comparan las áreas de estos polígonos para comprobar la relación
pitagórica.

PITÁGORAS Y EL TANGRAM

OBJETIVO

Comprobar geométricamente la validez del Teorema de Pitágoras por equivalencia entre áreas de figuras planas, en el caso particular del triángulo rectángulo isósceles.

ORGANIZACIÓN DE LA CLASE

En equipos de 3 o 4 personas

MATERIALES

Piezas de 3 Tangrams y visualizar la siguiente figura

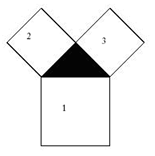
CONSIGNA

Empleando las piezas de 3 Tangram tenéis que probar que el área del cuadrado 1 es igual a la suma de las áreas de los cuadrados 2 y 3

PREGUNTA

¿Qué conclusión sacáis? Dibujad vuestra solución en papel, escribid vuestra conclusión y entregadlo con el nombre de todos lo componentes del grupo