ÁNGULOS EN LAS FIGURAS GEOMÉTRICAS
ÁNGULOS EN CUALQUIER POLÍGONO
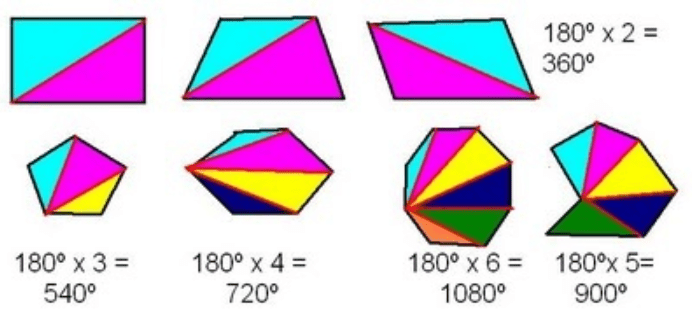
La suma de los ángulos internos de un polígono sigue la fórmula 180º*(n-2) siendo n el Nº de lados que tenga el polígono.
En el cuadrilátero, n = 4 lados; (n – 2) = 2 triángulos; SUMA = 360°.
En el pentágono, n = 5 lados; (n – 2) = 3 triángulos; SUMA = 540°.
En el hexágono, n = 6 lados; (n – 2) = 4 triángulos; SUMA = 720°.
En el icosaedro, n = 20 lados; (n – 2) = 18 triángulos; SUMA = 3240°
….etc
ÁNGULOS EN LOS TRIÁNGULOS
Los triángulos son polígonos de 3 lados y la suma de sus ángulos interiores es 180º y la de sus ángulos exteriores suma 360º
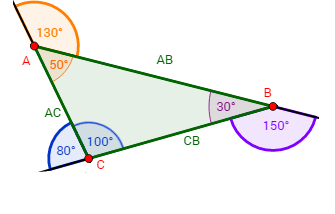
En el caso del triángulo vemos que también se cumple la fórmula 180*(n-2)=180*(3-2)=180*1=180º
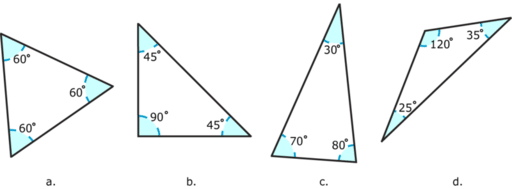
ÁNGULOS EN LOS TRIANGULACIÓN DE POLÍGONOS
Como sabemos que la suma de de los ángulos internos del triángulo es 180º solo tendremos que multiplicar 180 por el número de triángulos que podamos formar, que siempre será los lados de un triángulo menos 2 (ya que todos los triángulo menos dos compartirán 2 caras).
ÁNGULOS EN LA CIRCUNFERENCIA
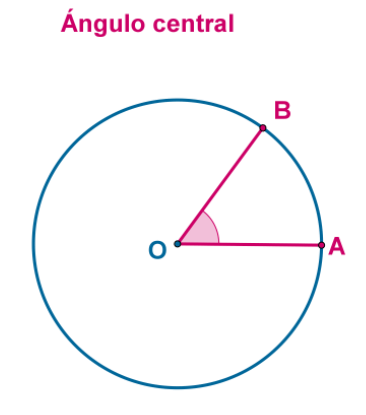
Ángulo central
Un ángulo central de una circunferencia es un ángulo cuyo vértice coincide con el centro de la circunferencia.
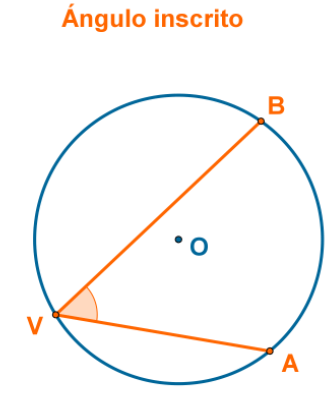
Ángulo inscrito
Un ángulo inscrito es el formado por dos secantes a la circunferencia.
ÁNGULOS INSCRITOS CON EL MISMO ARCO
Los ángulos inscritos en una circunferencia que abarquen el mismo arco tienen la misma medida

Prueba tu mismo
MEDIDA DEL ÁNGULO INSCRITO
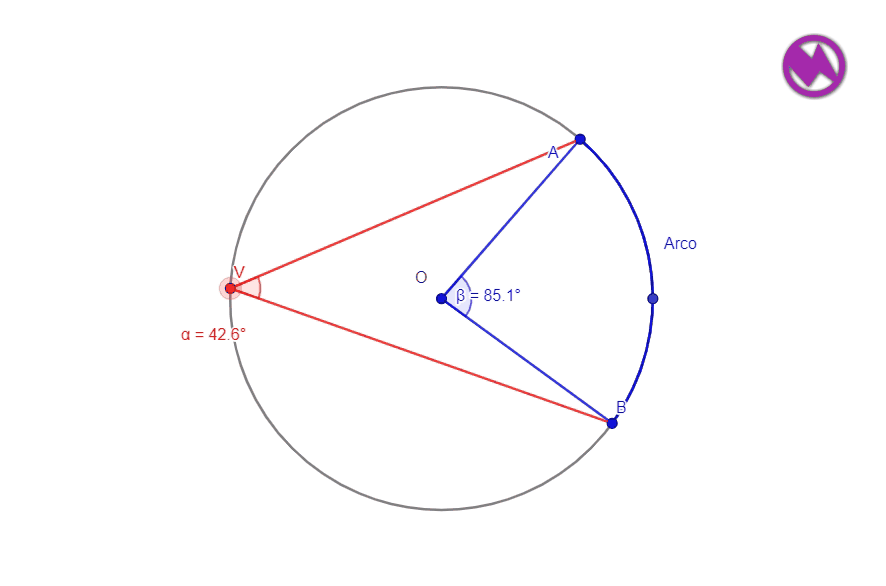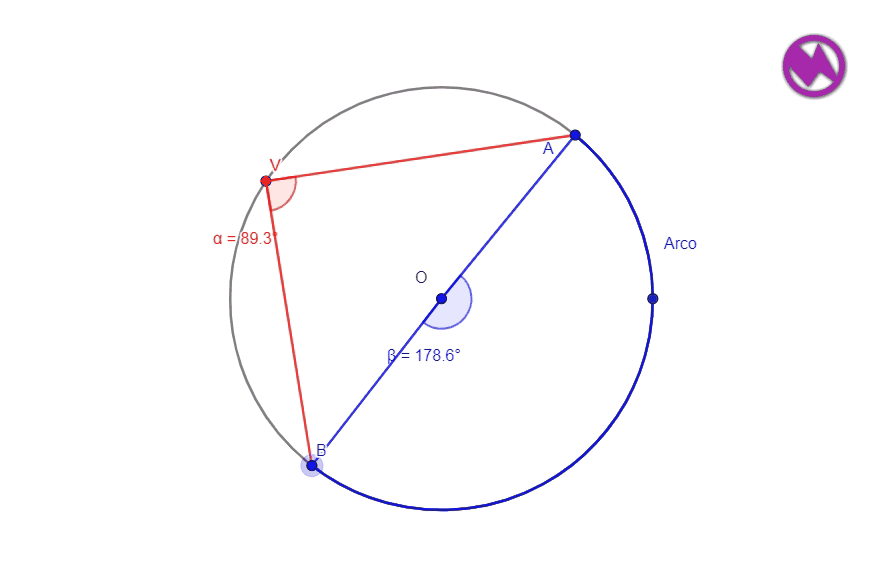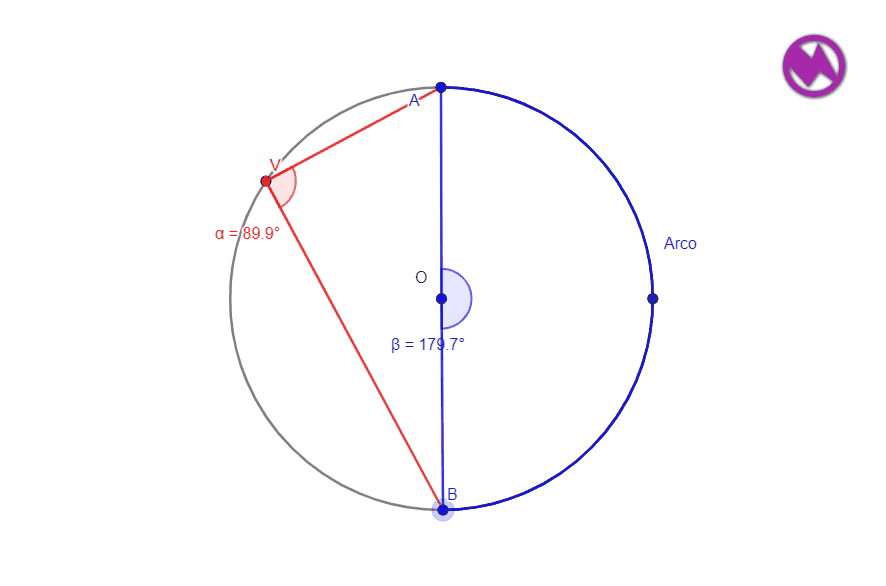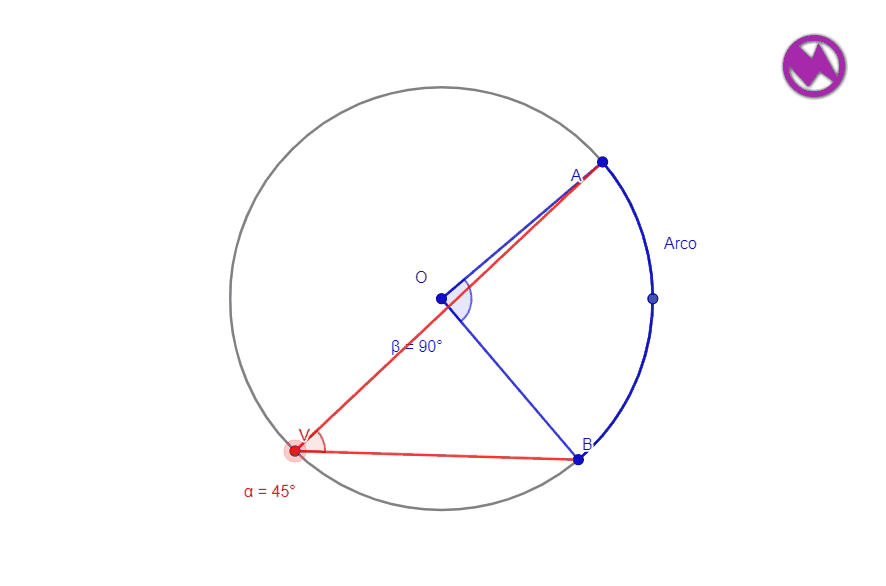
La medida de un ángulo inscrito es la mitad que la medida en grados que abarca el arco que forma.
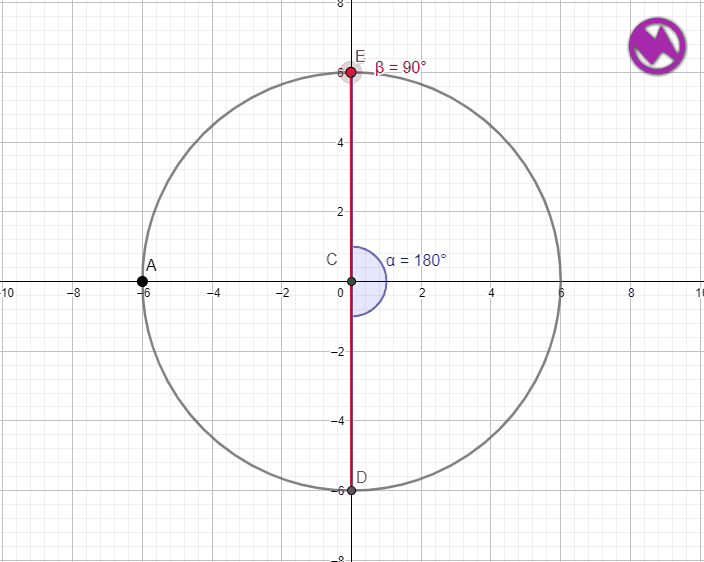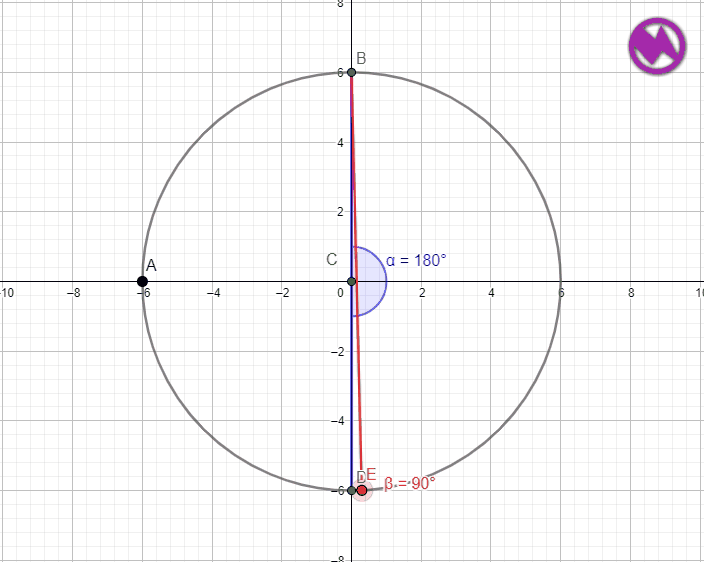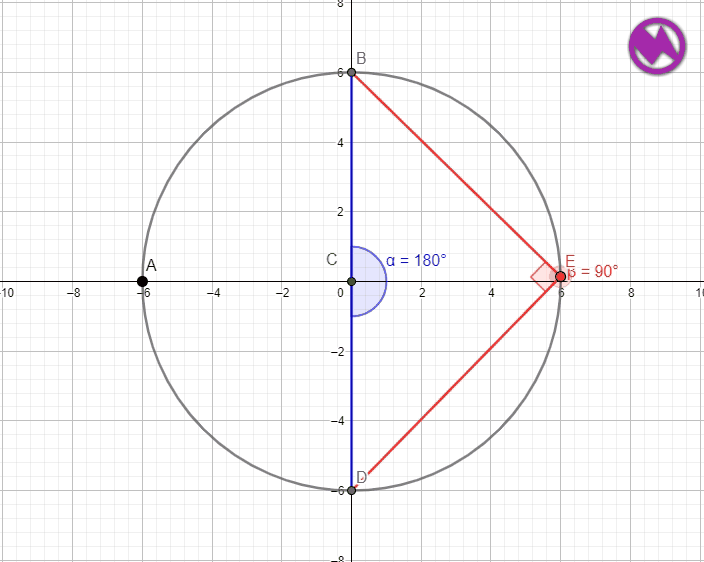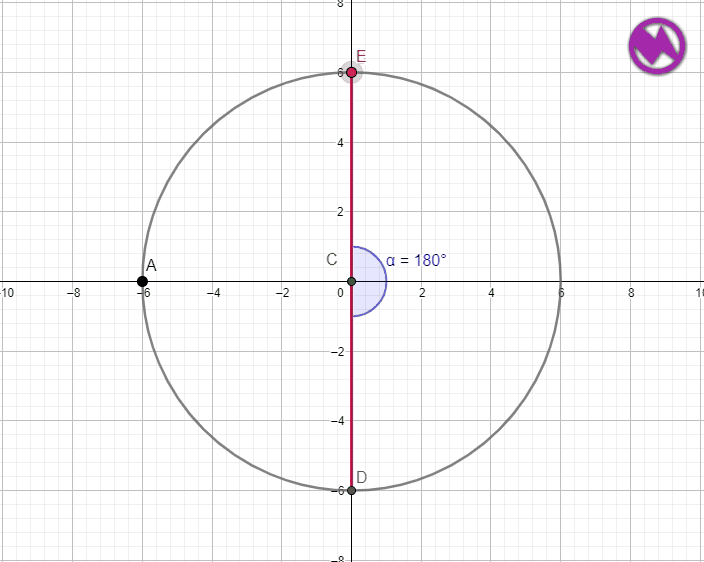
MEDIDA DEL ÁNGULO QUE ABARCA LA SEMICIRCUNFERENCIA
Una semicircunferencia está tiene por arco el diámetro de la misma la medida de ese arco será por lo tanto 180º y como hemos visto antes el ángulo inscrito será 180º/2 =90º

Debe estar conectado para enviar un comentario.